Let me start with a simplified case of a swimmer on a flat block, even if the old-style blocks weren't exactly flat. If the swimmer wants to dive off, he must push on the block to accelerate into a dive. Here is a diagram showing the swimmer and the forces on the swimmer during a start

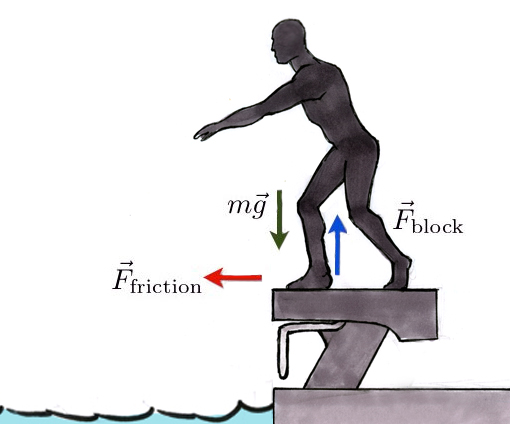
Yes, a swimmer typically grabs the block with his hands during a start. I will get to that in a moment. For now, let's consider this simple version. There are three forces on a swimmer: the gravitational force, the force of the block pushing up and the friction forward pushing in the direction of the acceleration. Remember, these are forces on the swimmer, not forces the swimmer exerts on the block.

Let me assume that during this starting motion, the swimmer only accelerates horizontally with no jumping up. In this case, the sum of the forces in the vertical direction (which I will call the y-direction) must add up to the zero vector. The basic principle of force says forces change the motion of an object. Since the vertical motion doesn't change (stays at rest) the net force must be zero.

This can be written:

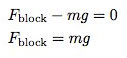
Now what about the horizontal direction? There is one force acting in the horizontal direction, friction. In almost all cases, the magnitude of the frictional force can be modeled with the following expression:

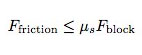
Where μs is the coefficient of friction. It is a value that depends upon the two types of materials interacting via friction (in this case, a human foot and a slightly abrasive material on the surface of the block). The harder the two surfaces are pushed together (Fblock) the greater the maximum value of the frictional force. What about the "less than or equal to" sign in the equation? That simply means this is the frictional force that tries to prevent the two surfaces from sliding. It will push only has hard as necessary (up to a point) to prevent sliding.

So, in the horizontal direction the only force is friction.

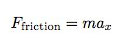
If the swimmer wants to win, he will push right at the limit of the maximum frictional force (but if he pushes too hard, he will slip). This means I can use the maximum frictional force and reduce the problem.

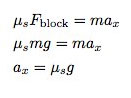
So the maximum horizontal acceleration just depends on the coefficient of friction. For now, I will estimate a friction coefficient of about 0.8, but it doesn't really matter what it is.

Block with Wedge

So what happens if there is a wedge at the back of the block? Again, let me simplify the situation just to show the difference. Let me assume the whole block is tilted at an angle θ above the horizontal. That will just change the force diagram like this:

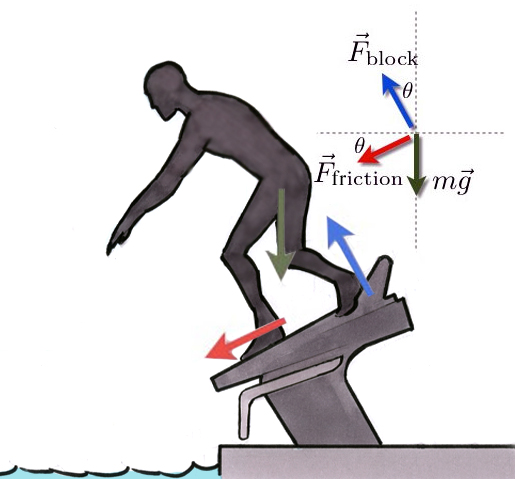
I drew the forces twice so it's easier to see how they add up. In this case, there are two forces that can accelerate the swimmer in the horizontal direction — both the frictional force and the force from the block. If I write the net force in both the x- and y-directions, I get:

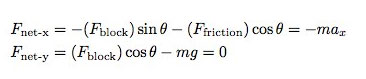
Here, the negative signs for the x-forces are there just because I drew the swimmer accelerating to the left. Now I will use the same model for the frictional force to solve for the acceleration in the x-direction.

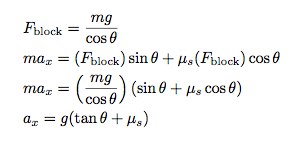
I know this looks crazy, so let's check a couple of things. First, does it have units of acceleration? Yes. Both of the trig functions have no units and neither does the coefficient of friction – that just leaves the acceleration with the same units as g. Second, what about the case where θ = 0? This should give the same result as before (since it is the same case). The tangent of zero (degrees or radians, it doesn't matter) is zero. So, yes, it gives the same result.

It isn't so easy to see how this acceleration changes with higher wedge angles. Let me plot the maximum acceleration for angles up to 30 degrees.

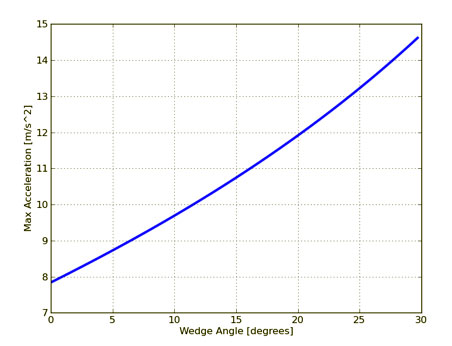
You can see it allows for a greater acceleration off the starting block. Of course, this is just a model since in reality the swimmer only has one foot on the wedge and one on the normal block. Hopefully, you get the idea.

What About the Hands?

When a swimmer grabs the front of the starting block, it does two things. First, the swimmer can push with his hands as well as his feet for greater acceleration. Second, the swimmer also can pull up on the block. This increases the force the block pushes on the swimmer and increases the frictional force, which also increases the starting acceleration.

Source www.swimmingfile.com